At around 04:15 UTC on 2022/1/15 the Hunga Tonga–Hunga Ha’apai Volcano exploded in the Pacific Ocean. A devastating event for anyone close by, and the tsunami generated affected seal levels anywhere with a pacific coast line.
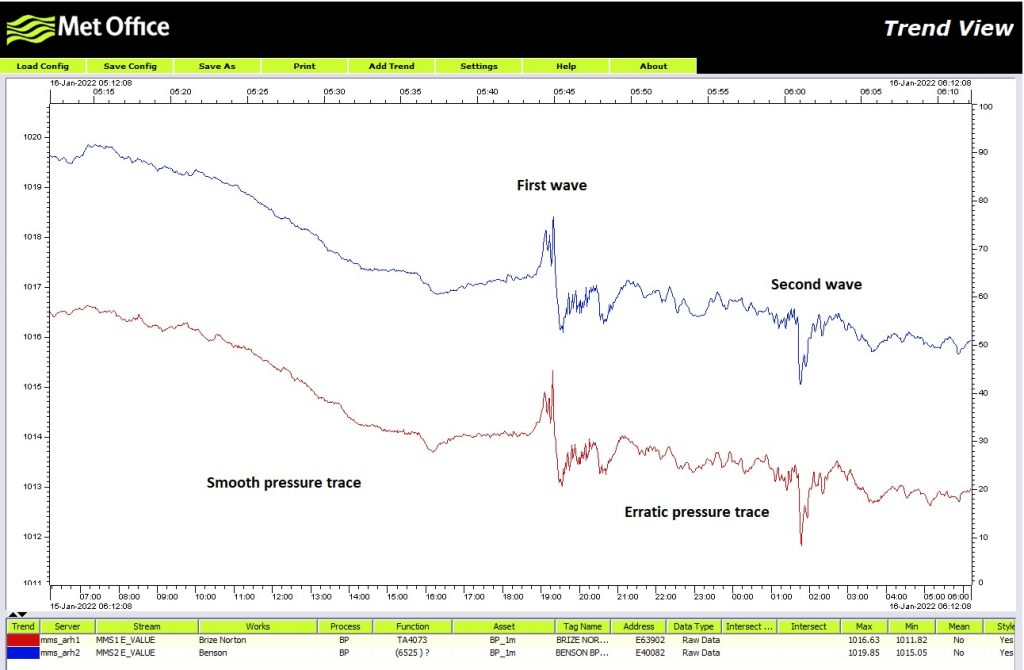
The satellite videos of the eruption show a pressure wave spreading out ahead of the dust cloud. The Met Office tweeted this morning that they had detected the pressure wave with their network of manometers.
I run a small personal weather station, I built around a raspberry pi 4 and a collection of sensors including a BME680 device which can monitor air pressure. I looked at the data collected yesterday and can see a positive spike in the local pressure at around 19:20 UTC, with an negative spike at 01:52 UTC on 2022/1/16.
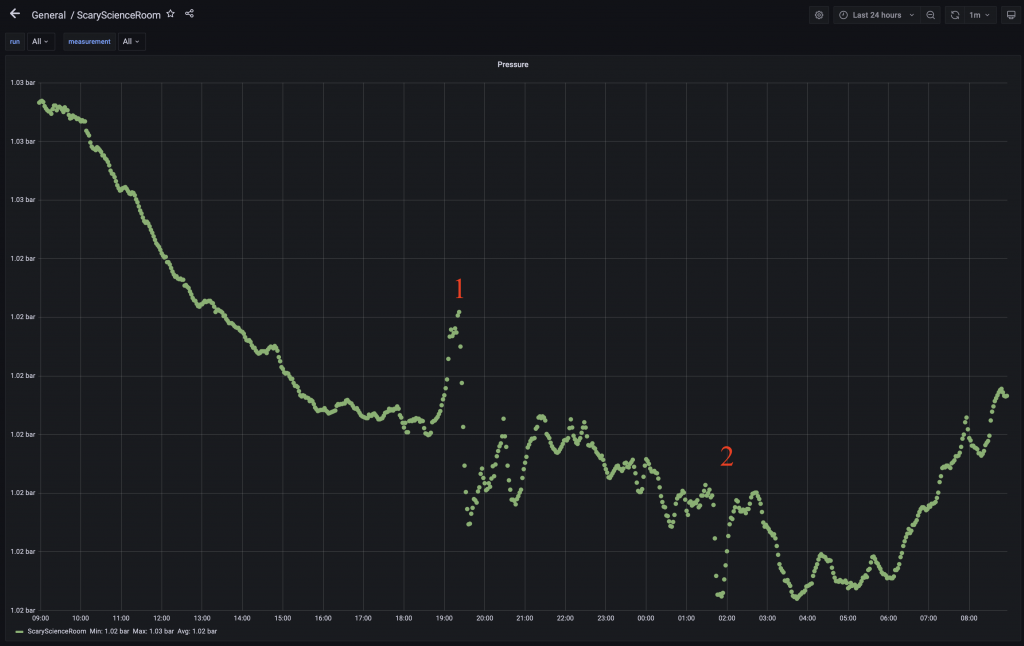
My house is 16,546 km from the eruption centre (the shortest path, is over the north pole – Earth is a sphere), knowing this and the time the pressure wave arrived, we can calculate the speed of the pressure wave.
The difference between the pressure wave being created and it being detected is 15h 5 min or 54,300 seconds.
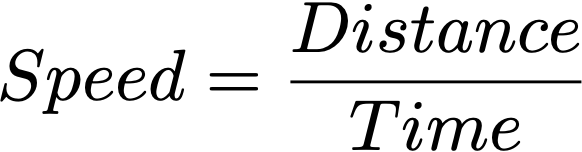
Substituting values gives us a speed of 0.305 km/s or 305 m/s, close to, but not quite the speed of sound (~340 m/s).
The second, negative going spike is the pressure wave that took the longer path to me, it travelled roughly 7000 km more, so arrived somewhat later. The various “noise” in the measured pressure between the two spikes is due to pressure waves arriving via other paths.
Taking the difference in time between the first and the second pressure wave arriving, and knowing the circumference of the Earth (40,075 km), I can get a pretty accurate measurement of the distance to the eruption.
The first pulse took 54,300 seconds to arrive, the second took 77,940 seconds. The average speed can be calculated for the pulse to travel one complete one circumference of the Earth, substituting into the equation before with
D = 44,075 km
T = 54,300 + 77,940 sec
Gives speed = 0.303 km/sec or 303 m/s
Solving for distance, using this speed and the time taken for each pulse to arrive, gives a shortest distance to the eruption of 16,542 km and a longest distance of 23,615 km. In pretty good agreement with the distances measured from the map.
